
| Introduction | |
To use the revised PRS prototype specification successfully, the agency must understand the implications of each decision made while developing or using the specification. These include general PRS decisions such as selecting the distress indicators used to define performance and the AQC's chosen to be included for acceptance, as well as more specific items such as defining appropriate values for the required constant variables. This chapter is designed to provide the typical user of the specification with the practical information required to make intelligent PRS-related decisions.
| Defining Pavement Performance | |
As previously stated, an underlying concept of a PRS is that knowledgeable decisions related to pavement lot acceptance and corresponding pay adjustments are based on the predicted pavement performance. In fact, the PRS is driven by key distress indicators. In the current PRS approach, pavement performance may be defined in terms of the development of any or all of the following distress indicators:
- Transverse joint spalling.
- Transverse joint faulting.
- Transverse slab cracking.
- Pavement smoothness over time (expressed in terms of PSR or IRI).
When developing a PRS for a given project, the agency must choose any or all of these distress indicators to define the pavement's performance. Those distress indicators not included in the chosen definition of performance will not be subjected to trigger values and, therefore, will not result in any responsive M & R activities or associated costs. For example, if transverse slab cracking is not included in the agency's definition of performance, slab replacement costs will not be incurred. It is recommended that all four of these distress indicators be used to define the pavement's performance.
| Selection of Included AQCs | |
Along with defining a pavement's performance by selecting distress indicators, the agency must also decide which AQC's are to be sampled and tested for acceptance. To make these selections, the agency must be aware of the interdependent relationships between distress indicator models and AQC's (these relationships are shown in figure 1). For example, if an agency includes transverse slab cracking in its definition of pavement performance, it is recommended that the agency choose to measure slab thickness and concrete strength since they are both key factors in the transverse slab cracking distress indicator model. If the agency were to choose not to sample an AQC that is required by a chosen distress indicator model, distress predictions would be made by holding that particular AQC at its target mean value. The revised PRS allows pay adjustments to be based on the measurement of any or all of the following five AQC's:
- Concrete strength (affects transverse joint faulting, transverse
joint spalling, and transverse slab cracking directly; affects pavement
smoothness indirectly).
- Slab thickness (affects transverse joint faulting and transverse
slab cracking directly; affects pavement smoothness indirectly).
- Entrained air content (affects transverse joint spalling directly;
affects pavement smoothness indirectly).
- Initial smoothness (affects pavement smoothness over time
directly).
- Percent consolidation around dowels (affects transverse joint faulting directly; affects pavement smoothness indirectly).
Based on the agency's selected definition of pavement performance, intelligent decisions must be made to define what AQC's are to be included in the PRS. It is recommended that the agency first identify those AQC's that are included in the selected distress indicator equations, as indicated above. From those included AQC's, the agency is encouraged to measure only those AQC's that it currently feels comfortable measuring. If this final selected list of AQC's greatly differs from AQC's required for the selected distress indicator models, it is recommended that the agency revisit its choices for included distress indicators. Because of the existence of these interdependent relationships between included distress indicator models and measured AQC's, the selection of both should be looked at as an iterative process.
| Identification of Constant Variable Values | |
Any developed PRS should be project-specific because the predicted
performance of any pavement is directly dependent on project-specific
variables. These variables fall into three categories: design-related
characteristics, climatic characteristics, and applied traffic loads.
Variables representing each of these three categories are used in the
agency-chosen distress indicator models to predict pavement performance.
These variables are labeled constant because they do not change
between the as-designed and as-constructed pavements. (Note: Figure
1 shows a list of the constant variables required by each distress
indicator model.)
Once the governing agency identifies the distress
indicator models used to define pavement performance and the AQC's to be
accepted, the next step is to assign values to the required constant
variables that represent the project's specific design, traffic, and
climatic conditions. In an effort to help agencies with the selection of
appropriate constant variable values, brief descriptions of each of the
possible constant variables are included below. The variables are divided
into the three main categories (design, climatic, and traffic) for
clarification.
Pavement Type—Although the current specification is only valid for JPCP, the agency must identify whether the chosen pavement design is to be constructed with or without dowel bars.
Road Location—Calculated user costs (vehicle operating costs) are dependent on the roughness of the pavement over time, as well as the location of a road.(13) The road location setting is defined as either rural and urban.
Lane Configuration—Calculated user costs are also dependent on the identified lane configuration of a road.(13) The lane configuration is defined as a combination of road type (divided or undivided) and total number of lanes (includes all travel lanes in both directions). Divided pavements are those in which the traffic traveling in opposite directions is divided by a barrier or median. The current approach allows the agency to select from the following six different lane configuration choices:
- 2-lanes, undivided pavement.
- 4-lanes, undivided pavement.
- 4-lanes, divided pavement.
- 6-lanes, divided pavement.
- 8-lanes, divided pavement.
- 10-lanes, divided pavement.
Initial Design Life—The total expected amount of time for which the chosen pavement design is expected to carry traffic loads without the application of a global rehabilitation (AC overlay, PCC overlay, diamond grinding). This is the initial design life used in the common pavement design procedures.
Analysis Period—Period of time over which future M & R costs are to be considered in an LCC analysis. The analysis period is typically defined as twice the chosen design life (as a minimum) to ensure that future impacts of M & R are considered.
Lane Width—The agency must define the individual widths of each traffic lane. Typical pavements are constructed using traffic lanes that are 3.7 meters in width. However, many agencies are now constructing widened outer traffic lanes (typically 4.3 meters in width) in an attempt to reduce the development of transverse slab fatigue cracking. The defined lane widths are used to calculate sublot and lot areas. The presence of a widened outer traffic lane is an input required by the transverse joint faulting and transverse cracking models.
Average Transverse Joint Spacing—The transverse joint faulting, transverse joint spalling, and transverse slab cracking distress indicator models all have average transverse joint spacing as a required input. JPCP's are typically constructed using constant joint spacings (e.g., every 4.6 meters) or random joint spacings (e.g., using a repeated pattern of 4.0-4.3-4.6-5.2 m). If a constant joint spacing is used, the constant value is used as the average transverse joint spacing in the distress indicator models. If a random joint spacing is selected, the appropriate transverse joint spacing is set equal to the mean of the joint spacings included in the repeated series. For example, a random joint spacing series of 4.0-4.3-4.6-5.2 m would have a mean transverse joint spacing value of 4.5 m.
Effective Modulus of Subgrade Reaction (k-value)—An effective subgrade k-value is a required input for the transverse joint faulting and slab cracking distress indicator models. The appropriate value for use in these models is the effective modulus of subgrade reaction (including seasonal variations) calculated for design purposes. (Note: This value is for the subgrade, not the top of base.) Additional information on determining an appropriate effective subgrade k-value is contained in appendix HH of Volume 2 of the 1993 AASHTO Guide for Design of Pavement Structures.(14)
Base Type—The specified base type is a required input for the transverse joint faulting model. The current approach allows the agency to select from the following granular (unbound) and stabilized base types:
- None.
- Asphalt-treated aggregate.
- Cement-treated subgrade.
- Cement-treated aggregate.
- Crushed stone, gravel, or slag (untreated).
- Gravel (uncrushed).
- Lean concrete.
- Lime-treated subgrade.
- Limerock.
- Pozzolanic-aggregate mixture.
- Sand.
- Soil aggregate mixture.
- Soil cement.
Dowel Diameter—If the pavement is selected to be constructed with dowel bars, the agency must identify the dowel diameter. The dowel diameter is a required input in the transverse joint faulting distress indicator model and is expressed in units of mm.
Base Permeability Factor—Information regarding the permeability of the base material is required for the transverse joint faulting model. This model includes a base permeability dummy factor as an input. This dummy variable is set equal to 0 when the base is not considered to be permeable and is set equal to 1 when the base is considered to be permeable.
PCC Modulus of Elasticity—The transverse joint faulting model requires a value for the PCC modulus of elasticity. The appropriate modulus of elasticity is expressed in units of MPa.
Mean Annual Daily Average Temperature—The transverse slab cracking distress indicator model requires knowledge about the mean annual daily average temperature. Although the distress model does not require this variable as a direct input, it is used by the agency, along with the average annual total precipitation, to determine the climatic region in which the project exists. Mean annual daily average temperature data are readily available from most climatic databases.Table 3. Identification of climatic regions in the United States based on mean annual average daily temperature and average annual total precipitation.
Average Annual Total Precipitation—The average annual total precipitation is used in combination with the mean annual daily average temperature to determine the climatic region in which the project exists. Annual precipitation data are readily available from most climatic characteristic databases.
Average Daytime Thermal Gradient—An estimate of the average daily thermal gradient through the slab is a required input of the transverse slab cracking distress indicator model. An estimated thermal gradient value may be determined as a function of slab thickness and determined climatic region. The United States is divided into four climatic regions based on the mean annual daily average temperature and average annual total precipitation. The appropriate climatic region is determined using table 3. After determining the appropriate climatic region, an appropriate average daytime thermal gradient through the slab may be determined as a function of climatic region and design thickness using table 4.
|
Average Annual Total Precipitation |
Mean Annual Average Daily Temperature | |
|---|---|---|
|
£ 13 ºC |
> 13 ºC | |
|
£635 mm |
Dry-Freeze Region |
Dry-Nonfreeze Region |
|
> 635 mm |
Wet-Freeze Region |
Wet-Nonfreeze Region |
Table 4. Average daytime thermal gradient through the slab based on slab thickness and climatic region.(16)
|
Average Daytime Thermal Gradient, ºF/in | |||
|---|---|---|---|
|
Slab Thickness, mm |
Wet-Nonfreeze Climatic Region |
Dry/Wet-Freeze Climatic Regions |
Dry-Nonfreeze Climatic Region |
|
203 |
1.40 |
1.13 |
1.41 |
|
229 |
1.30 |
1.05 |
1.31 |
|
254 |
1.21 |
0.96 |
1.21 |
|
279 |
1.11 |
0.87 |
1.10 |
|
305 |
1.01 |
0.79 |
1.00 |
Note: The average daytime thermal gradients shown in this table are in units of ºF/in. The transverse slab cracking distress indicator model requires that the gradient be entered in these units.
1 ºC/cm = 4.572 ºF/in
Average Annual Number of Wet Days—The transverse joint faulting distress indicator model requires knowledge about the average annual number of wet days.Data for this variable are included in most available climatic databases.
Number of Days Above 90 ºF (32 ºC)—The average annual number of days in which the daily maximum temperature exceeds 90 ºF (32 ºC) is a climatic input required by the transverse joint faulting distress indicator model. Daily temperature data are readily available in most climatic databases.
Mean Freezing Index—The mean freezing index is a measure of the severity of frost for a region, expressed in terms of degree-days. The transverse joint faulting and spalling distress indicator models require the mean freezing index as a direct input. Although freezing index data are readily available in most climatic characteristic databases, values may be estimated for the continental United States using figure 13.
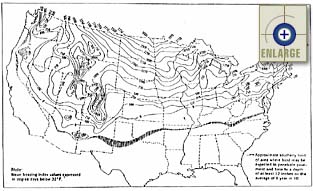 |
Figure 13. Distribution of mean freezing index values in the continental United States (Note: This chart is expressed in English units).(17) |
Annual Freeze-Thaw Cycles (at 7.6 cm below the surface)—The current transverse joint spalling distress indicator requires knowledge about the number of annual freeze-thaw cycles (FTC's) in the pavement (specifically, at 7.6 cm below the pavement's surface). It is to be noted that the number of "in pavement" FTC data is much different than the typically reported number of "air" FTC's. However, it has been found that the number of "in pavement" FTC's may be reasonably estimated from the measured daily maximum temperatures. One "in pavement" FTC may be assumed to occur whenever the measured daily maximum temperature stays at or below freezing (0º C) for at least 2 consecutive days (48 hours).
For example, if consecutive daily maximum temperatures were to read 4, 0, –1, 6 (all in ºC), this would constitute one "in pavement" FTC since the temperature stayed at or below freezing on days 2 and 3 (0 and –1 ºC, respectively). If the consecutive daily maximum temperatures were to read 2, 0, –1, –4, –8, 4 (all in ºC), this would still constitute only one "in pavement " FTC since the temperature stayed at or below freezing on days 2 through 5 (0, –1, –4 and –8 ºC, respectively). However, a series of consecutive daily maximum temperatures reading 2, 0, 5, –2, 5 (all in ºC), results in zero "in pavement" FTC's since the maximum daily temperature stayed at or below freezing for only 1 day (0 on day 2).
Transverse Joint Sealant Type—The transverse joint spalling model is dependent on the type of transverse joint sealant material selected for use on the pavement. In the current approach, the agency may choose from the following three sealant types:
- None (transverse joints are not sealed).
- Liquid asphalt sealant.
- Preformed compression seal.
Presence of Salt—Research in a previous study showed that the development rate of transverse joint spalling was significantly increased when salt (calcium chloride) was used for deicing purposes.(1) The presence of salt was, subsequently, included as an input in the current transverse joint spalling distress indicator model. The agency must, therefore, identify if salt (calcium chloride) is regularly used on the pavement.
Total Cumulative Design ESAL's—The transverse slab cracking and transverse joint faulting models are very much dependent on the number of ESAL's expected to be applied over the analysis life of the pavement.The current PRS approach requires knowledge about the total number of ESAL's expected to be applied in the pavement's first year of service or the total cumulative number of ESAL's to be applied over the pavement's design life. Either one of these values, in combination with information on the identified traffic growth pattern (discussed below), allows for the calculation of the ESAL's expected to be applied in every year of the pavement's analysis life. The current PRS approach also allows for the calculation of these yearly ESAL values based on known average daily traffic (ADT) information.
Traffic Growth Pattern—The agency must define the traffic growth rate and growth type for a given pavement project. The growth rate defines the annual increase in the applied yearly ESAL's (expressed as a percentage). The defined growth type determines how that percentage is applied and is selected by the agency as either simple or compound.
Simple Growth Type Method—If the agency selects a simple traffic growth type, the traffic is assumed to follow a linear relationship over time. Yearly ESAL values using the simple growth method may then be determined using equation 8.
whereESAL n = ESAL I + (n – 1) * [ESAL I * (Rate /100)] (8)
ESAL n = Estimated applied ESAL's at year n.
ESAL I = Initial ESAL's applied during year one of the pavement's service life.
n = Year of pavement service life for which ESAL's are being calculated.
Rate = Chosen traffic growth rate, expressed as a percentage (e.g., if 7.5% is the chosen growth rate, "Rate" = 7.5).
Compound Growth Type Method—If the agency selects a compound traffic growth type, each year's traffic increase is assumed to be calculated as a constant percentage of the previous year's applied ESAL's (compounded). Yearly ESAL values using the compound growth method may then be determined using equation 9.
whereESALn= ESAL I * [1 + (Rate /100)](n – 1) (9)
ESAL n = Estimated applied ESAL's at year n.
ESAL I = Initial ESAL's applied during year one of the pavement's service life.
n = Year of pavement service life for which ESAL's are being calculated.
Rate = Chosen traffic growth rate, expressed as a percentage (e.g., if 7.5% is the chosen growth rate, "Rate" = 7.5).
| Selection of AQC Target Values | |
Identifying the as-designed AQC target values (means and standard
deviations) is one of the most important tasks facing the governing
agency. These chosen target AQC's are used to define the agency's desired
pavement quality. In the current PRS approach, this desired quality is
defined as the quality for which the agency is willing to pay 100 percent
of the contractor-submitted bid price. If the contractor constructs a
pavement that is measured to have better AQC quality than that defined by
the as-designed target AQC's, then (on average) the contractor will
receive an incentive payment (greater than 100 percent of the bid price).
Conversely, if the as-constructed AQC pavement quality is measured to be
less than that defined by the as-designed AQC target values, then (on
average) the contractor will receive a disincentive payment (less than 100
percent of the bid price).
Initially, it is recommended that the
PRS quality levels (AQC target values) be set to represent the quality
levels specified under the agency's current specifications. If appreciably
lower quality levels are specified for the target values, the result will
be decreased performance. If appreciably higher quality levels are
specified, contract bid prices are likely to increase. While such higher
quality levels (with attendant higher bid prices) might well result in
lower overall LCC's, it would be difficult for an agency to justify
increases in specified quality without the agency first having some
experience with PRS (i.e., knowledge of the effect of specified quality on
bid price and expected performance).
For an agency to select AQC
target levels that represent the quality levels currently being specified,
the agency must have a thorough understanding of its current
specifications, and particularly its acceptance plans.The agency must
first identify the AQC quality levels (means and standard deviations) for
which its current acceptance plans are asking. Sometimes, these quality
levels are not obvious. In fact, the currently specified quality levels
may be different than what the agency actually desires (i.e., something
other than what the agency intended to specify). To identify exactly what
quality level the agency is currently specifying, the agency's expected
payment (EP) curves should be utilized. The EP curve is a graphic
representation of an acceptance plan that shows the relation between the
actual quality of a lot and its expected pay.(4)That quality
level (on an EP curve), for which the agency is willing to pay 100 percent
of the contractor-submitted bid price, should be interpreted as the
currently specified quality level for each AQC. If the agency has not
developed EP curves, computer programs are currently available (such as
R.M. Weed's OCPLOT) to assist the highway agency in their
development.(18) If the agency acceptance plan cannot easily be
converted to an EP curve, it is suggested that the agency develop a new
acceptance plan so that the SHA can clearly determine the quality level
currently being specified. The new acceptance plan should, of course,
consider the typical quality levels being achieved by contractors in the
State.
The agency-defined AQC target values are dependent on the
chosen AQC acceptance sampling and testing plan. The recommended AQC means
and standard deviations may change based on test type and number of
replicate test results. For example, if concrete strength were being
measured using 28-day cylinder compressive strengths, the AQC target
values would be very different than those recommended for the case where
28-day beams were being tested for flexural strength. It is important to
have knowledge of the proposed acceptance sampling and testing plan prior
to construction so that the appropriate AQC target values can be
defined.
As stated previously, initially, the target means should
be selected to be equal to the AQC values for which the contractor would
expect to receive 100 percent pay. Ideally, these values should correspond
to the values used for design purposes. Target standard deviations should
be determined by analyzing historical AQC data or by referring to
published estimates of standard deviations (appendix D has a number of
recommended values from the literature and field and laboratory testing
conducted under this project). If the agency has a reasonable amount of
good historical data representative of an AQC, it is strongly recommended
that the agency analyze these data to determine appropriate AQC target
means and standard deviations. The following steps can be used to
determine target values based on historical AQC construction data:
- Identify an AQC for which target values need to be determined (e.g.,
concrete strength).
- Identify the sampling and testing type to be used for accepting the
AQC in the field (e.g., cylinders from material taken from in front of
the paver).
- Identify historical projects that not only use the same sampling and
testing types, but are also believed to have been constructed with AQC
quality matching that desired by the agency.
- Compute the sample mean and unbiased standard deviation of all of
the representative sample test results (from each sample location) for
each project. Sample means are computed using equation 5.
Unbiased sample standard deviations are computed using equation 6. The
target standard deviation includes both testing and process or materials
variation.
- Analyze the computed project AQC unbiased standard deviations and use them to identify appropriate AQC target standard deviations. (Note: The computed sample means should be checked against the assumed target means.) The computed data should give the agency knowledge about what type of quality has been provided on similar paving projects by the contractors. It is up to the agency to interpret these results and decide on appropriate AQC target means and standard deviations that define the true quality desired.
Although historical data should ideally be used to determine appropriate AQC target means and standard deviations, the initial recommendations for determining these values are summarized in table 5.
Table 5. Initial recommendations for determining AQC target means and standard deviations.
|
Acceptance Quality Characteristics |
Initial Recommendations for Target Mean |
Initial Recommendations for Target Standard Deviation |
|---|---|---|
|
Concrete Strength |
The target mean should be interpreted from a developed EP curve. This value should be equal to the current agency mean strength input used in the pavement design procedure (see note 1). |
These values should be based on historical project testing data. If no historical data are readily available, the values may initially be based on published data, or on the laboratory and field data collected under this research study (see appendix D). Both the variations due to testing and to materials should be included. See note 4. |
|
Slab Thickness |
The target mean should be interpreted from a developed EP curve. This value should be equal to the current agency design thickness determined from the pavement design procedure (see note 2). | |
|
Entrained Air Content |
The target mean should be set equal to the current agency-designed entrained air content. This AQC is only significant in areas with significant freezing temperatures. | |
|
Initial Smoothness |
The target mean should be interpreted from a developed EP curve. See note 3. | |
|
Percent Consolidation Around Dowels |
The target mean should be determined from testing conducted by the agency to determine typical levels achieved, or from published data (see). |
- Notes:
- The AASHTO Guide for Design of Pavement Structures
requires a flexural strength, third-point loading, 28 days curing
(Mr). If another testing type is selected for the AQC (such
as 28-day cylinder compressive strength [f'c]), then a
correlation using the project materials must be established and
utilized. For example, if the design input to AASHTO is 4.48 MPa
flexural strength, and the correlation is f'c =
(Mr/0.83035)2, then the corresponding target mean
would be based on a design compressive strength of 29.13 MPa. If
strength at any other time than 28 days is desired for the AQC, then
correlations with maturity must be established for the project
materials.
- Most design procedures, such as the AASHTO design
procedure, include a formal engineering reliability design provision.
Others include various safety factors. Either of these approaches result
in a slab design thickness that already includes a large safety factor
or high design reliability. Thus, the design slab thickness is the mean
slab thickness that is desired in the field, not an arbitrarily
increased value.
- The value specified here for the profile index (PI)
should be related to the level of initial PSR specified for the AASHTO
design procedure. The lower the PI specified, the higher the design
initial PSR.
- The standard deviation is highly dependent upon the number of replicate tests involved. For example, if the mean of two concrete cylinders (both from one batch of concrete) represents one test for a site, the standard deviation for this case will be less than for the case when only one cylinder is used to represent the site. Typical standard deviation values obtained from field projects are discussed in appendix E.